سخت ترین مسائل ریاضی حل نشده؛ از فرضیه ریمان تا P درمقابل NP
سخت ترین مسائل ریاضی حل نشده؛ از فرضیه ریمان تا P درمقابل NP در حوزه ریاضیات، همواره مسائلی وجود دارند که به دلیل پیچیدگی زیاد، تاکنون نتوانستهایم آنها را حل کنیم. این مسائل شامل مسائلی معروف مانند فرضیه ریمان و مسئله P درمقابل NP هستند. ۴ مورد از سخت ترین مسائل ریاضی حل نشده عبارتند […]
سخت ترین مسائل ریاضی حل نشده؛ از فرضیه ریمان تا P درمقابل NP
در حوزه ریاضیات، همواره مسائلی وجود دارند که به دلیل پیچیدگی زیاد، تاکنون نتوانستهایم آنها را حل کنیم. این مسائل شامل مسائلی معروف مانند فرضیه ریمان و مسئله P درمقابل NP هستند. ۴ مورد از سخت ترین مسائل ریاضی حل نشده عبارتند از:
۱. فرضیه ریمان
فرضیه ریمان یکی از بزرگترین مسائل حوزه ریاضیات است که هنوز توسط هیچ ریاضیدانی حل نشده است. این فرضیه به ما میگوید که تمامی صفرهای تابع زتا ریمان، اعدادی مختلط هستند که بخش حقیقی آنها برابر با ۱/۲ است. تاکنون تلاشهای فراوانی برای اثبات یا رد این فرضیه انجام شده است، اما هنوز پاسخ قطعی درباره صحت آن داده نشده است.
۲. مسئله P درمقابل NP
مسئله P درمقابل NP یکی از مهمترین مسائل محاسباتی است که تا به امروز نتوانستهایم به طور قاطع به آن پاسخ دهیم. مسئله P درمقابل NP به بررسی این سؤال میپردازد که آیا مسائلی وجود دارند که به طور سریع و بازدهی خوب قابل حل شوند (در زمان چندجملهای) یا خیر؟ اگر چنین مسائلی وجود داشته باشند، آنها را مسائل P مینامیم؛ و اگر تنها راه حلهایی باشند که بازدهی زمانی بدتری دارند (غیرچندجملهای)، آنها را مسائل NP مینامیم. تاکنون تلاشهای بسیاری برای بررسی این مسئله صورت گرفته است، اما هنوز پاسخ قطعی درباره آن به دست نیامده است.
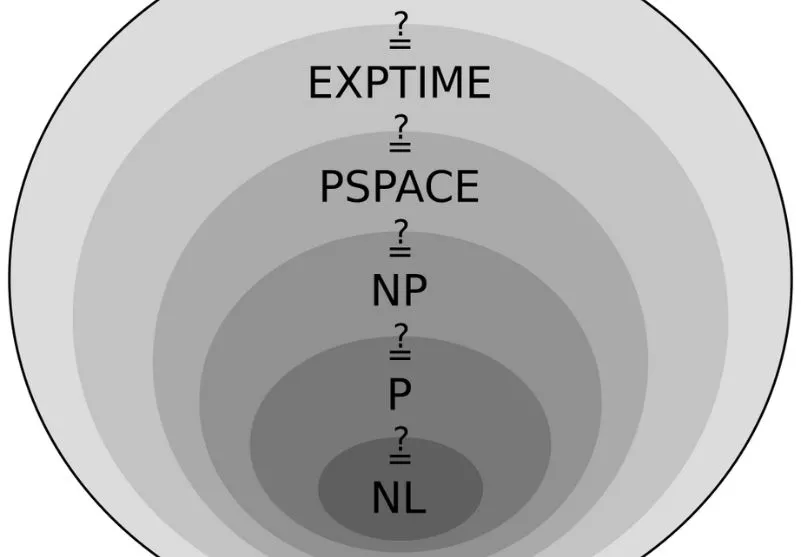
۳. مسئله همونگی از سخت ترین مسائل ریاضی حل نشده
مسئله همونگی یکی دیگر از مسائلی است که تاکنون حل نشده است. این مسئله مربوط به بررسی این سؤال است که آیا یک دستگاه همونگی خطی با n مجهول و n معادله قابل حل است یا خیر؟ تاکنون الگوریتمهایی برای حل این مسئله وجود دارد، اما هیچ کدام از آنها به طور کامل و برای همه موارد به جواب میرسند.
۴. فرضیه P = NP
فرضیه P = NP یکی از معروفترین فرضیههای محاسباتی است که تا به امروز هنوز به طور قاطعی اثبات یا رد نشده است. این فرضیه بیان میکند که هر مسئلهای که با استفاده از الگوریتمی بازدهی چندجملهای قابل حل باشد، تعداد کارهای غیرچندجملهای نیز وجود داشته باشد که با استفاده از آنها مسئلههای NP نیز قابل حل شوند. اگر این فرضیه ثابت شود، به این معناست که تمامی مسائل NP نیز قابل حل هستند و الگوریتمهای بازدهی چندجملهای برای آنها وجود دارد.
در این مقاله، به بررسی چندین مسئله ریاضی که تا به امروز حل نشدهاند، پرداختیم. مسائلی همچون فرضیه ریمان، مسئله P درمقابل NP، مسئله همونگی و فرضیه P = NP
همچنان چالشهای بزرگی برای ریاضیدانان به همراه دارند. امیدواریم که در آینده، با پیشرفت علم ریاضی و روشهای جدید، بتوانیم این مسائل را حل کرده و به دستاوردهای بزرگی در علم ریاضی و کاربردهای آن دست یابیم.

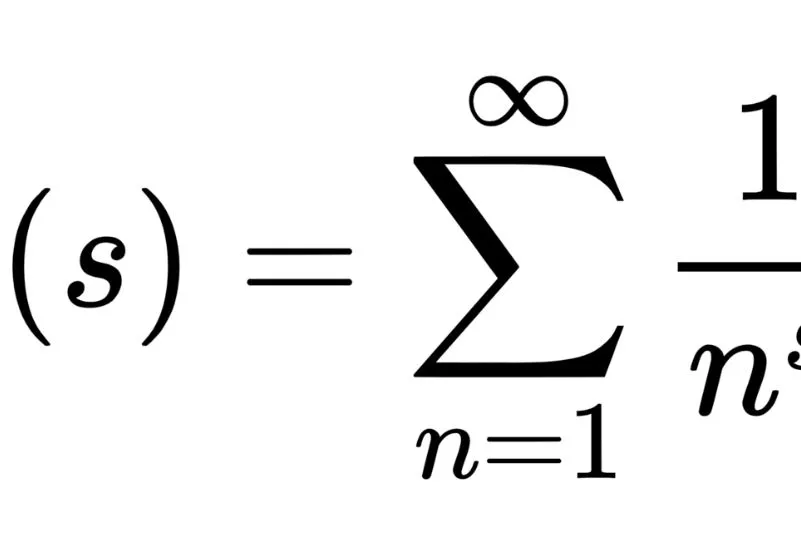




ارسال دیدگاه
مجموع دیدگاهها : 0در انتظار بررسی : 0انتشار یافته : 0